Le circuit-LC.

Vous trouverez ici les circuits LC considérés du point de vue radio-électricité...Les circuits LC jouent un rôle essentiel dans tous les systèmes électroniques radiofréquences.

Ce sont surtout des notions d'analyse harmonique, c'est à dire concernant les réponses en fréquences. Les circuits LC sont en effet indispensables pour la conception des cartes RF , notamment en tant que filtres ou adaptations ( Vous trouverez ces notions détaillées dans le chapitre Couplage de deux circuits LC, filtre LC).
Il vous sera également utile de bien maîtriser les circuits LC pour le routage de ces cartes de radiocommunications, car les phénomènes parasites sont souvent liés à des inductances et des capacités non désirées auxquelles on ne pense pas toujours... Vous pensez connaître les circuits LC ? Jetez un œil ci-dessous, il se peut que vous y trouviez une approche inattendue

L’association d'une inductance (appelée aussi self) et d'un condensateur est à l’origine de phénomènes de résonance. Utilisé pour réaliser des filtres ou pour adapter des impédances, le circuit LC produit aussi de nombreux phénomènes pas toujours désirés.
Nous ne reviendrons pas sur les calculs qui permettent de retrouver les résultats de l'association d'une inductance et d'un condensateur en utilisant leurs impédances complexes jLw et -j/cw.
La formule de Thomson que l'on trouve partout donne la fréquence de résonance d'un circuit LC en fonction de L et de C.
Mais il est très souvent commode de la considérer différemment, avec les unités utilisées en RF : Fréquence en GHz - Capacité en pF - inductance en nH.
La formule pratique devient : (f²)=25,4 / LC
Exemple : C= 10pF L = 100 nH alors on trouve f=0,159 GHz soit donc 159 MHz.

Plaçons la self et le condensateur en série. Nous appellerons cette association «circuit résonant série».
L’impédance de ce circuit série est nulle à la fréquence de résonance.

On peut être choqué par le fait que deux impédances en série ont une impédance nulle !....Cela s'explique très bien si on considère l'impédance jLw de l'inductance et l'impédance -j/cw du condensateur. Si on les met en série, la somme de ces deux impédances jlw-j/cw s'annule pour un certain w.

Plaçons la self et le condensateur en parallèle. Nous appellerons cette association « circuit résonant parallèle ».
L’impédance de circuit parallèle est infinie à la fréquence de résonance.

Circuit résonnant amorti :

Cependant, en général, les condensateurs et les selfs ne sont pas parfaits : résistance ohmique de la self, rayonnement de la self, pertes diélectriques du condensateur, etc… De plus, le circuit n’est pas isolé : on aura connecté en parallèle sur ces composants des éléments résistifs pour faire fonctionner le système. Le résultat de tout cela, c’est que l’énergie des oscillations électriques sera plus ou moins dissipée. On dit que le circuit résonnant est « amorti »

L’amortissement du circuit peut être mesuré par le « coefficient de surtension » noté Q: Un circuit peu amorti possède un Q élevé.

Circuit résonnant série :

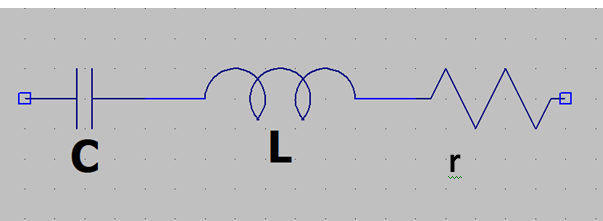
Toutes ces pertes peuvent être représentées, autour de la fréquence de résonance, par une résistance pure fictive r en série dans le circuit LC.
La conséquence, c’est qu’à la fréquence de résonance, l'impédance du circuit série ne sera plus tout à fait nulle, il subsistera cette résistance en série notée ici par r. Cette résistance est d'autant plus petite qu'il y a peu de pertes.

Circuit résonnant parallèle :

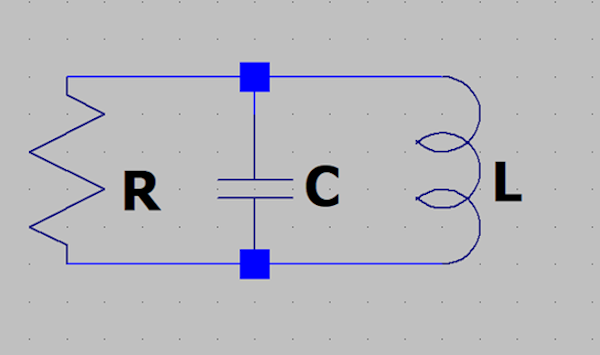
Toutes ces pertes additionnées peuvent être représentées, autour de la fréquence de résonance, par une résistance pure fictive R en parallèle sur le circuit LC. Donc, à la fréquence de résonance, même si l'ensemble LC présente une impédance infinie, il subsistera cette résistance.
Cette résistance d'amortissement est d'autant plus grande qu'il y a peu de pertes.

Remarquons que le circuit résonnant peut être considéré parallèle ou série, selon l'emplacement de la charge.
La différence, c'est que dans le circuit parallèle nous modélisons l'amortissement par une résistance parallèle (grande) et que dans le circuit série, nous modélisons l'amortissement par une résistance en série (petite).

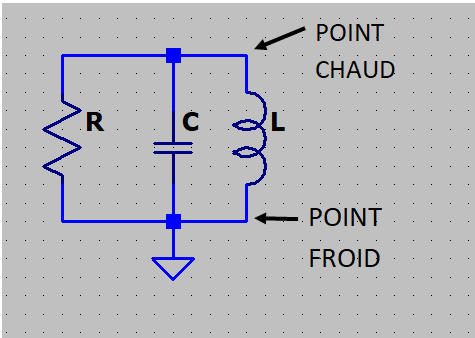
Définition du point chaud, du point froid...

Un circuit LC est généralement introduit dans un réseau constitué de nombreux composants, et comprenant une référence, la masse. Cette masse est sous forme d'un plan métallique constituant la "couche de masse" de la carte électronique.

Le "point froid " d'un circuit LC possède une impédance nulle par rapport à cette masse soit parce qu'il y est relié directement, soit parce qu'il y est relié par un condensateur d'impédance nulle en RF, dit "condensateur de découplage". Il n'y a donc pas de tension RF sur un point froid.

Le "point chaud" d'un circuit LC possède une impédance maximale par rapport à la masse. S'il y a de l'énergie RF dans ce circuit, c'est en ce point que la tension est maximale.

Nous parlons de point chaud ou de point froid en général en supposant qu'il y a résonance.
Il est important de bien comprendre ceci : À la fréquence de résonance, les impédances n'ont qu'une partie réelle :
elles sont équivalentes à des résistances pures. Donc l'impédance" au point chaud d'un circuit à la résonance est équivalente à une grande résistance. Nous verrons par la suite que cette résistance fictive au point chaud est utile pour déterminer les autres résistances présentées par les différents points du circuit LC. Pour ceux qui pratiquent la RF depuis longtemps, le point chaud est reconnaissable si on le touche du doigt, c'est le point le plus sensible, l'endroit où le doigt "désaccorde" le circuit. Mais attention s'il y a une tension élevée !

Nous voyons que dans ce circuit, la résistance au point chaud, c'est tout simplement la grande résistance parallèle R dont nous avons parlé plus haut, puisque l'ensemble de L et C en parallèle a une impédance infinie.

En dehors du point chaud, de résistance maximale, et du point froid de résistance nulle, nous pouvons trouver sur un circuit (à la fréquence de résonance) des résistances intermédiaires. Par exemple, si on fait une prise au milieu de la self,le point situé sur cette prise présentera une résistance R/4, (si R est la résistance au point chaud.) Nous verrons cela en détail au chapitre Les adaptations par circuit LC

Rappelons-nous qu'à la résonance, ces impédances qu'on voit n'ont qu'une partie réelle, ce sont des résistances, même si souvent on continue à parler d'"impédance".

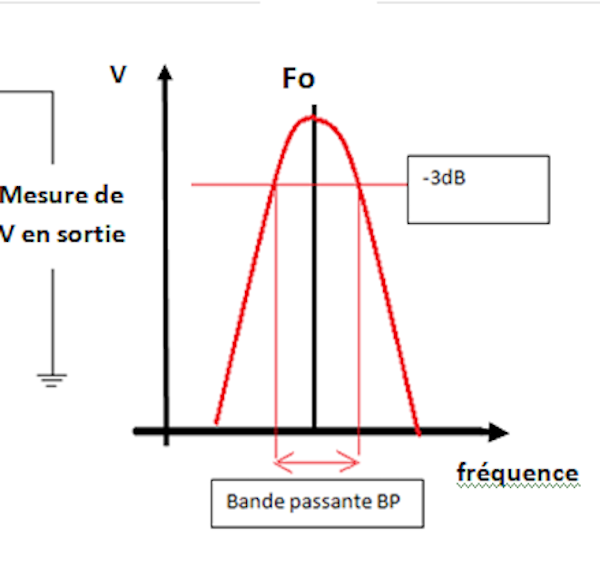
Courbe de réponse - Coefficient de surtension

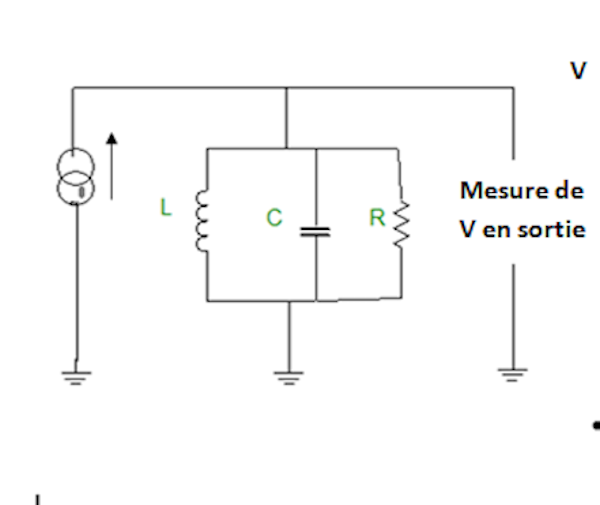
La figure ci-dessous montre le montage d'une manipulation ultra classique d’un «circuit LC parallèle» attaqué par un générateur de courant i.
Ce circuit réel est modélisé par une self parfaite L, un condensateur parfait C, et une résistance R qui représente l’amortissement.

A la fréquence de résonance, l’ensemble «L et C en parallèle» a une impédance infinie. Donc à la fréquence de résonance, l'ensemble composé de L et de C disparaît, il ne reste que la résistance R, et l'impédance de l’ensemble sera R, et sera maximum.
La tension de sortie sera alors égale au courant injecté multiplié par R. Comme R est grand, cette tension peut être très grande .

Imaginons la réponse en fréquence de ce système. La tension est maximale à la fréquence de résonance Fo, puisque L et C ont "disparu" à cette fréquence. Dès qu'on s'écarte un peu de la fréquence de résonnance, l'ensemble LC n'a plus une impédance infinie, et l'impédance totale de l'ensemble RLC commence à baisser.
Appelons BP (bande passante) la largeur du pic de la courbe (à -3dB) de la réponse en fréquence. Le rapport Fo / BP indique combien la courbe est « pointue ». Ce rapport de la Fréquence à la bande passante est le coefficient de surtension Q du circuit LC.

Par exemple, si Fo = 20 MHz et si BP = 0,5 MHz, alors Q = 20/0,5 = 40

Remarque : Il est possible de calculer ce coefficient Q d’une autre façon :

À la fréquence de résonance, l’impédance de la self et l’impédance du condensateur ont le même module, qu’on appellera Z.

Nous avons vu plus haut que l'amortissement peut être représenté, à la fréquence de résonance, soit par R, la résistance équivalente parallèle (grande), soit par r, la résistance équivalente série r dans le circuit LC (petite)

On peut exprimer le coefficient de surtension :

• soit par : Q = R/Z
• ou encore par Q = Z/r

Relation entre la résistance parallèleR et la résistance série r d'un circuit résonnant:

Ces deux expressions de Q permettent de trouver une relation entre R et r. Donc on sait transformer R en r et réciproquement, avec une précision d’autant plus grande que Q sera grand. En pratique, il faut que Q soit au moins égal à 3.

On a alors : r.R = Z².

C’est le transformateur en L, qui permet de transformer une résistance grande en résistance petite, et réciproquement.

Notons que ces formules sont approchées, mais d'autant plus précises que Q est grand. Pour des Q faibles, de l'ordre de 1 ou 2, l'abaque de Smith (voir chapitres Les lignes de transmission et Les adaptations par circuit LC ) donnera des résultats plus précis.

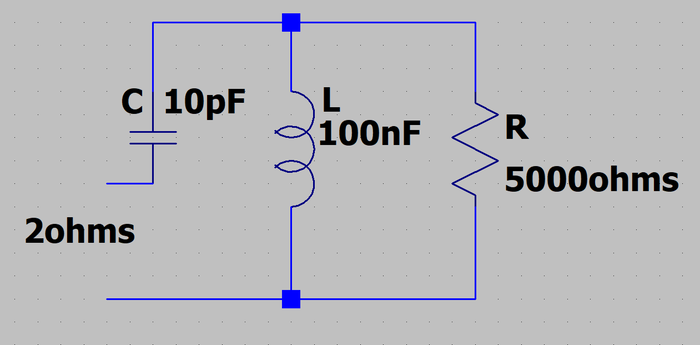
Exemple : considérons le circuit ci-dessous.
Un circuit composé d’une inductance L et d’un condensateur C sans pertes est chargé en parallèle par R = 5 000Ω. L’inductance est de 100 nH et le condensateur est de 10 pF.

Question : À la fréquence de résonance, quelle résistance r voit-on en série ?

Le calcul de lafréquence de résonance donne : Fo = 160 MHz

La fréquence de résonance est la fréquence à laquelle l’impédance de C et l’impédance de L sont égales en modules :

Ici, à la fréquence de résonance Fo = 160 MHz, on trouve que L et C ont une impédance de module Z = 100Ω.
On a r.R = Z². Donc r = 10 000/5000 = 2Ω (è la fréquence Fo, bien sur !)

On a donc transformé une résistance de 5000Ω (à droite) en une résistance de 2Ω (à gauche).

Réciproquement, si nous plaçons une résistance de 2Ω en série (à gauche sur le schéma), alors apparaîtra une résistance de 5000Ω en parallèle (à droite sur le schéma)

Le circuit en L, sur sa fréquence de résonance, est donc un "transformateur" de résistances. Nous verrons au chapitre Les adaptations par circuit LC tous les transformateurs possibles à l'aide d'un circuit LC.

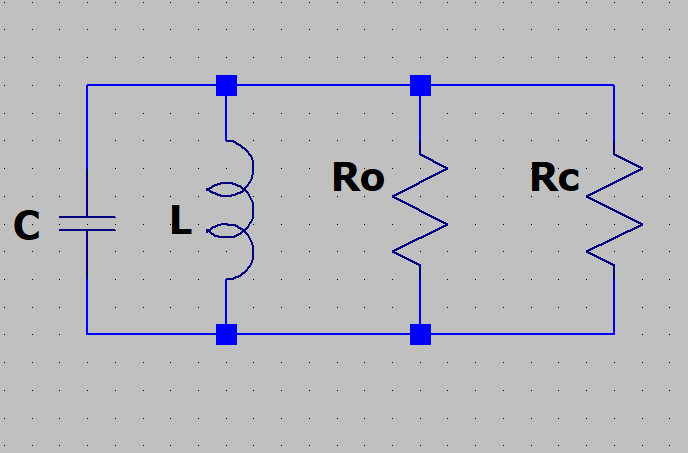
Coefficient de qualité à vide et coefficient de qualité en charge

Le coefficient de surtension Q d’un circuit LC est du à deux causes d’amortissement :

1. La qualité des composants LC, les selfs et les condensateurs n’étant jamais parfaits, ils dissiperont une partie de l’énergie qu’ils reçoivent. Il s’agit essentiellement de la résistance ohmique de la self, des pertes par rayonnement, de la qualité du diélectrique du condensateur, etc... Toutes ces pertes propres au circuit lui-même donnent ce qu’on appelle le Q à vide du circuit LC, noté Qo. Si L et C sont en parallèle, à la fréquence de résonance, on peut représenter cet amortissement propre au circuit par une résistance fictive Ro en parallèle, très grande si les composants sont de bonne qualité.
2. Les « charges » du circuit LC : Le circuit LC n’est jamais isolé, il remplit une fonction, souvent celle de filtre, et donc il est associé à d’autres éléments électroniques dans un réseau. On dit qu’il est « chargé ».
   Ces "charges" sont des éléments plus ou moins résistifs, et sont constituées souvent par une résistance Rc en parallèle sur le circuit. On dit qu'on a "une charge parallèle".
   Cette charge fait donc baisser le coefficient de surtension, et on chargera donc un "circuit LC parallèle" par une résistance grande, si on ne veut pas trop "écrouler" le coefficient de surtension.

   Le coefficient de surtension réel, appelé Qc, (Q en charge), est donc donné par ces deux résistances en parallèle sur le circuit, Ro et Rc. Ces deux résistances amortissent le circui. Mais on comprendra que Ro est nuisible, puis qu’elle représente l'énergie dissipée dans la self et dans la capa, alors que Rc est utile, puisque le but est de transmettre l’énergie à cette charge.

   Ainsi, si Ro est très grand devant Rc, les pertes propres, dissipées par Ro, seront faibles. Par contre, si par exemple Ro = Rc, alors la moitié de l’énergie injectée sur le circuit sera dissipée et ne sera pas restituée par le circuit à la charge, le circuit fera perdre 3 dB.

   

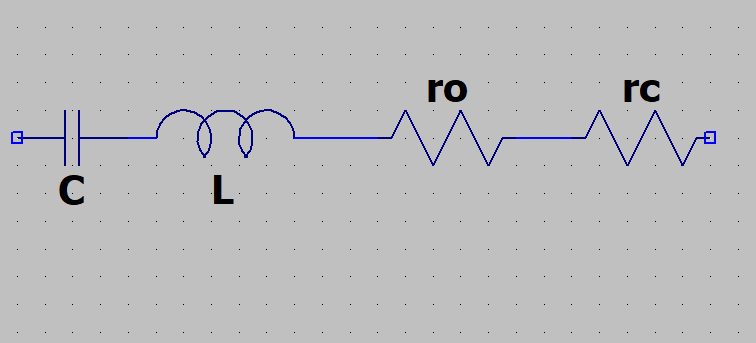
   Circuit série :

   On peut considérer non pas le circuit LC composé d'éléments en parallèle, mais composé d'éléments en série. C'est bien sur le même circuit : Le circuit série n'existera que s'il est rebouclé de façon à former une maille.

   Les pertes propres du circuit considéré "série" peuvent être représentées par une résistance série ro, d'autant plus que les composants sont de bonne qualité...

   Charges série :

   Parfois, le circuit doit transmettre son énergie à une charge de résistance petite. On choisira alors de placer cette charge en série dans le circuit LC.

   Cette charge rc s'ajoute à la résistance série ro due aux pertes propres au circuit. Dans ce cas, bien sur, la résistance totale en série ro + rc devra être bien plus petite que les impédances de L et de C, si on veut conserver un minimum de coefficient de surtension.

   

   Modélisation des selfs et des condensateurs du circuit LC, en vue d'une simulation :

   Il est généralement plus simple de prendre les modèles de self et de condensateur avec leur résistance série, et ce modèle sera valable même autour de la résonance.

   Modélisation de la self :
   En plus de la self inductance L, le composant réel qu'il faut modéliser comprend une résistance en série r qui représente les pertes, ( cette résistance croît avec la fréquence), et une capacité parasite en parallèle, sans oublier non plus les selfs parasites des deux connexions. Ces éléments parasites ont d'autant plus d'influence qu'on monte en fréquence...

   Modélisation du condensateur :
   Lui aussi possèdera une résistance parasite série, qui augmente avec la fréquence, et une self parasite due au boîtier et au corps du condensateur.
   Vous aurez plus de précisions concernant la construction de ces modèles dans les chapitres "Le condensateur en RF" et et L'inductance en UHF

   Identifier la "maille" de résonance

   Nous verrons dans le chapitre "Les adaptations par circuit LC", que le circuit LC résonant peut prendre des formes un peu plus complexes que la simple association d'une seule inductance et d'un seul condensateur. Ce seront des circuits en pi, des circuits en T, etc...

   Si le circuit LC comprend plusieurs condensateurs ou plusieurs inductances, et si le circuit présente un Q suffisant, il est important de bien identifier la maille de résonance, c'est à dire la maille dans laquelle le courant est plus élevé du fait de la résonance. Cela permettra en particulier de savoir si une charge résistive qui lui est connectée est "série" ou "parallèle".

   En effet, si on augmente la résistance, le Q augmentera si elle est "parallèle", et diminuera si elle est "série".

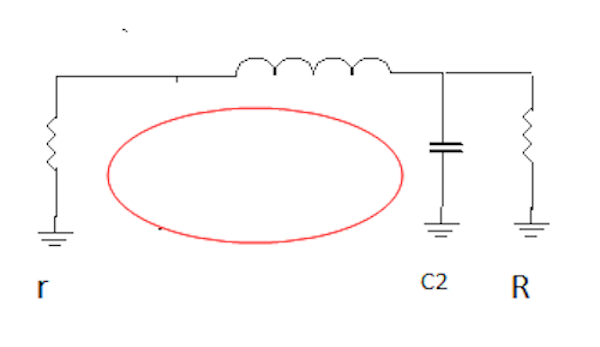
   Par exemple, l'ellipse montre la maille de résonance d'un circuit LC classique . On voit que la résistance r est une charge série ( r petit si Q grand) et on voit que la résistance R est une charge parallèle non parcourue par le courant de résonance ( R grand si Q grand)

   

   Un autre exemple, on voit que dans un circuit en "π", le courant de résonance traverse les deux condensateurs, ce qui veut dire que la capacité qui accorde la self est constituée de ces deux condensateurs en série. On voit que les deux résistances sont des charges parallèle (R grand si Q grand)

   

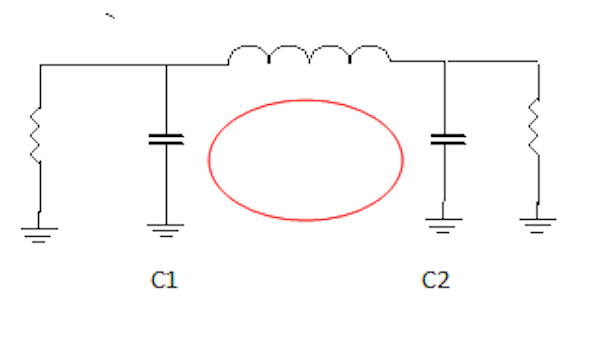
   Et si le Q est très bas ? Pour un réseau à faible Q ( Q < 3), nous verrons plus loin que la méthode par l'abaque de Smith donne des résultats plus précis.

   Le circuit LC utilisé comme transformateur.

   Ces deux exemples précédents nous montrent que le circuit LC permet de transformer une impédance RF en une autre. Il s'agit en fait de transformer une résistance en une autre, C'est à dire d'adapter une source ( ou générateur) de résistance interne R1 à une charge de résistance R2. C'est le circuit à la résonance qui permet cela. Du fait de cette résonance, le circuit LC effectuera également un filtrage entre la source et la charge.

   Une remarque: Lorsque la charge est adaptée à la source, charge et source provoquent le même amortissement du circuit.

   Le chapitre sur les adaptations par circuit LC vous montrera les différentes façons d'utiliser un circuit LC en adaptateur d'impédance.

   Prenons un exemple, en circuits de radiocommunicatiopns:

   Un récepteur possède sur son entrée un étage à faible bruit (LNA : low noise amplifier) équipé d'un transistor à effet de champ (FET). Pour filtrer ce qui vient de l'antenne et pour l'adapter, nous voulons faire précéder ce transistor d'un circuit LC qui sera connecté en parallèle sur l'entrée du FET.

   L'impédance d'entrée du FET est donnée, équivalente à une résistance Re =3500Ω en parallèle sur une capacité de 4 pF.
   Le circuit LC , accordé sur 160 MHz a un Qo donné de 88 et comprend une inductance de 100 nH.

   Ci-contre le schéma.
   Comme l'impédance d'entrée du FET est grande, on la placera en parallèle sur le circuit LC.
   Nous pouvons évaluer la capacité qu'il faudra mettre en parallèle sur l'inductance pour obtenir la résonnance à 160 MHz :
   Il faut 10 pF pour accorder une self de 100 nH. Comme il y a déjà 4 pF dans l'entrée du transistor, il faudra placer 6 pF sur la self.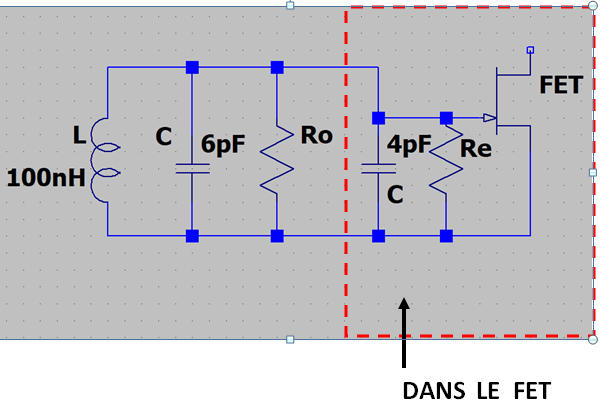

   

   Si on calcule l'impédance de la self 100 nH à 160 MHz, on trouve Z =LW = 100Ω

   Calculons la résistance de pertes propres au circuit LC :

   son Qo à vide est donné : Qo = Ro/Z

   --> Ro = Z.Qo = 100.88 = 8800Ω.

   La résistance parallèle totale sur le circuit est donc 8800Ω en parallèle avec les 3500Ω du FET, donc 2500Ω.

   Son Q en charge est donc : Qc = R/ Z = 2500/100 = 25 et sa bande passante : 160 MHz/25 = 6,4 MHz

   

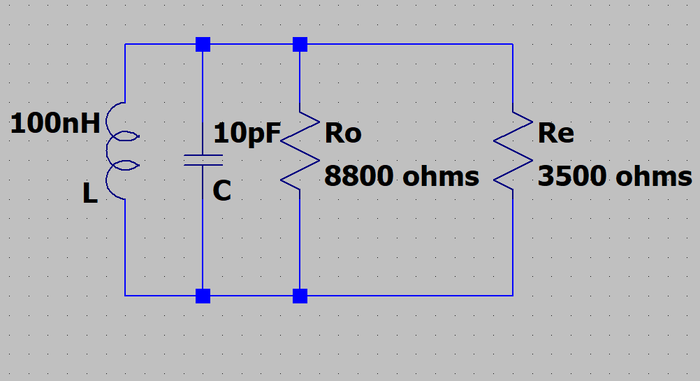
   On peut aussi à calculer les pertes de transmission de ce circuit LC : La puissance qui vient de l'antenne va se dissiper dans la résistance de 3500Ω du transistor (là, elle est utile) et dans la résistance Ro de 8800Ω due à la qualité du circuit LC (là, c'est dommage)

   Comme P = V²/R pour chaque résistance, la puissance totale est Ptot = V²/2500Ω et la puissance prise par le transistor est P utile = V²/3500. Ce qui fait Putile/Ptotale = rendement = 0,7 soit une perte de 10 log (0,7) = 1,5 dB

   On voit donc que ce circuit LC, de qualité moyenne, fait perdre 1,5 dB à l'ampli LNA. Si ce n'était qu'une perte de gain, ce ne serait pas grave, mais on perd sur le signal avant le transistor, donc on perd sur le facteur de bruit et sur la sensibilité !

   Ce n'est pas fini. Pour l'instant, le point chaud du circuit présente une résistance de 2500Ω. Or, notre antenne (plus exactement le câble coaxial qui apporte le signal) présente une résistance de 50Ω.

   Le chapitre "Les adaptations par circuit LC" indique tout ce qui est possible de faire pour transformer les résistances.

   Nous allons ici faire une prise surla self pour réaliser un autotransformateur.

   On veut transformer les 2500Ω du point chaud en 50Ω, soit un rapport de résistances de 2500/50 = 50, donc un rapport du nombre de spires de racine de 50 = 7.

   La prise antenne se fera donc à 1/7 de la bobine. S'il y a 7 spires, ce sera à une spire de la masse.

   

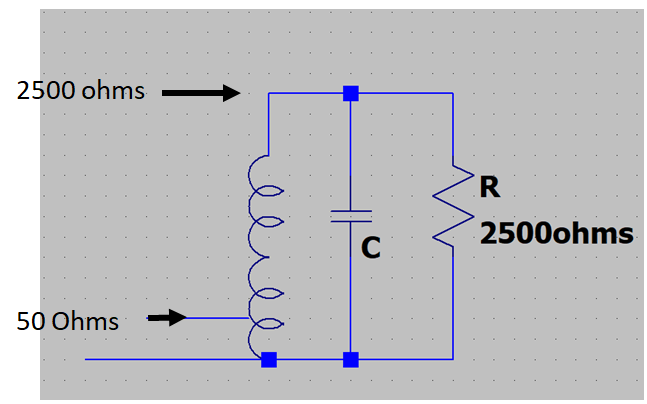
   Dernière remarque : maintenant, le circuit LC est amorti également par l'antenne. Son Qc sera divisé par deux et sa bande passante sera de 12,8 Mhz..

   Phénomènes à la résonance :

   La résonance va produire des phénomènes qu'il faut bien connaître :

   La « surtension » à la résonance :
   À l’aide d’une source de tension, appliquons une tension RF sur un « circuit LC série> ». À la fréquence de résonance, le circuit série se réduit à la résistance série r, qui est petite si le Q est élevé. La source de tension est donc appliquée sur cette résistance très petite. Donc le courant est très important. Mais ce courant traverse quand même la self L et la capacité C donc nous aurons aux bornes de L et aux bornes de C une tension bien plus importante que celle appliquée par le générateur.

   >Rappelons qu'on a appelé «point chaud» le point d’un circuit résonant LC où la tension (ou l'impédance) est la plus élevée par rapport à la masse.

   Le « sur-courant » à la résonance : Appliquons une tension sur le sommet ( point chaud) d'un circuit résonant parallèle. Cette tension va provoquer un courant dans la self et un courant dans le condensateur. Mais ces deux courants sont égaux mais opposés,ce qui signifie que le courant sortant de la self est le même que celui entrant dans le condensateur. Le courant qui vient du générateur est donc, uniquement le courant allant dans la résistance en parallèle, il est très faible si R est grand.

   Le circuit LC est donc le siège d'un courant bien plus important que celui que lui injecte le générateur. Nous verrons qu’il est important de connaître ce phénomène lors du routage des composants sur une carte (chapitre Routage et CEM des cartes radio).

   Choix de L et de C D'un circuit résonnant.

   Comme la fréquence de résonance est fonction du produit LC, on peut se poser la question :
   Puisque c'est le produit qui compte, ais-je le droit de prendre ce que je veux pour L ou pour C ?
   Par exemple, si je choisis L très petit, il suffira que je place alors un C très grand...

   Eh bien non, on ne peut pas faire n'importe quoi.

   Si je diminue fortement L, l'inductance diminuera plus vite que la résistance du conducteur (*Si je diminue le nombre de spires d’une bobine, son inductance décroît plus vite que le nombre de spires, alors que la résistance décroît proportionnellement aunombre de spires…),

   donc le Qo = ZL /r , sera réduit. Par ailleurs, en VHF et UHF, la piste constituera une self qui deviendra prépondérante.

   Si j’augmente fortement L, le Qo du à la self va certes augmenter. Mais la self possède une capacité parasite, et viendra un moment où cette capacité, additionnée aux capacités des pastilles du circuit imprimé, sera suffisante à elle seule pour réaliser l’accord sur la fréquence désirée. L'accord du circuit, réalisé par uniquement les capacités parasites par rapport à l'environnement, deviendra instable et difficilement modélisable. Par ailleurs, la résistance équivalente en parallèle sur L et C deviendra énorme : R = Q.Z, ce qui peut poser des problèmes.
   Cependant, le Qo du circuit étant maximum dans ce cas, on utilisera ces circuits avec C minimum pour réaliser des filtres à pertes minimales : ce sont les filtres en hélice.

   En règle générale, sauf cas particuliers, on choisit l'impédance Z de la self et de la capacité (elles ont le même module Z à la résonance) entre une vingtaine d'Ω et quelques centaines d'Ω. C'est à dire, souvent, autour de la centaine d'Ω.

   Un exemple decas particuliers, si le circuit LC attaque un transistor RF de puissance. L'impédance d'entrée d'un tel transistor peut être très petite, de l'ordre de l'ohm voire moins. Cette charge sera placée en série dans un circuit LC d'adaptation. On voit que si on veut une bande passante pas trop étroite, il faudra un circuit LC d'impédances Z faibles. Par exemple, un circuit avec ZL =, Zc = 10Ω et une charge série de 1Ω aura un Q de 10. Pour plus de détails sur cet exemple, voir le chapitre Exemple : "Un ampli UHF de puissance"

   Mesurer la fréquence de résonance d’un circuit LC sur une carte.

   Il est parfois nécessaire d’avoir une idée de la fréquence de résonnance d’un circuit LC déjà en place sur une carte électronique. Il existe à cet effet des « ondemètres » à absorption, ou « grid-dip ». On couple la bobine du grid-dip à la bobine du circuit à mesurer, et en balayant les fréquences d’oscillation du grid-dip, on trouve une déviation de l’aiguille car à sa fréquence d’accord, le circuit testé absorbe l’énergie du grid-dip.

   Pour que la mesure soit correcte, il faut que le montage soit sous tension, car les charges et les capacités des semiconducteurs sont différentes quand le circuit n’est pas sous tension.

   On peut aussi utiliser un analyseur de spectre avec tracking, et un coupleur directif :
   À la fréquence de résonance, une boucle couplée au circuit à mesurer présentera une variation du coefficient de réflexion.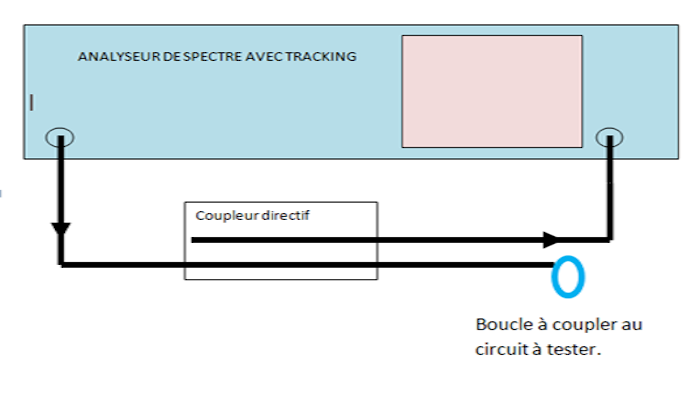

   

   Dans le paragraphe « L’inductance réelle », nous indiquons une autre façon de mesurer la fréquence de résonance de l’association d’une inductance et d’un condensateur ( mais hors de la carte), par la méthode « du réjecteur».

   Pourquoi une telle importance des circuits LC en radiofréquences ?

   1. Les circuits LC sont partout sur les cartes RF : Ainsi, par exemple, entre deux étages d’amplification RF, on trouvera des circuits LC qui servent à la fois de filtre et d’adaptation d’impédance.
   2. Notons au passage qu'aux fréquences de plusieurs centaines de MHz voire plus, les inductances et condensateurs notés sur le schéma théorique ne sont pas les seuls, les pistes présentent des inductances et des capacités dont il faut tenir compte. Parfois même, si on utilise des composants "répartis", les circuits LC seront composés uniquement de pistes. Par ailleurs, les composants eux-mêmes présentent des capacités et des inductances, que l'on intègrera dans le modèle de chaque composant.
   En conclusion, pour "router" une carte RF, il faut savoir tenir compte de ces éléments L et C parasites.

   Et en hyperfréquences ?

   Il existe plusieurs façons de passer aux résonateurs électromagnétiques en hyperfréquences :

   1. On pourra passer aux "cavités" fermées classiques en 3 dimensions.
   2. On pourra passer aux résonateurs micro-strip, qui ne sont rien d'autre que des cavités aplaties dont les bords sont ouverts au lieu d'être fermés...
   3. On peut tenter de rester en composants localisés, si on veut réduire les dimensions et si on n'a pas de problèmes de puissance, par exemple pour créer les circuits hybrides. On pourra réduire toutes les dimensions des inductances et des capacités, en appliquant le principe d'homothétie :

   Si on réduit dans le rapport k, les 3 dimensions spatiales de l'ensemble des composants, du routage, du substrat, des diamètres des conducteurs, on obtient alors des inductances et des capacités de valeurs divisées par k, et donc une résonance de fréquence k fois plus élevée (sauf le Qo qui est divisé par racine de k).

   Ces composants sont parfois utilisés sur les circuits hybrides, mais on arrive vite à des composants liliputiens au delà de quelques GHz. Et il est alors plus facile de créer des inductances imprimées